Mathematics of Generative Adversarial Network
In the previous post we discussed the basics of GANs. In today’s post we will delve right into the mathematics of the GAN.
Based on the zero sum non cooperative game. If one wins then the other loses. This zero-sum game is also known as a minimax game. Discriminator (\(D\)) is trained to maximize the probability of assigning the correct label to both training examples and samples from Generator (\(G\)). While the generator maximizes probability of (\(D\)) to make mistakes, by minimizing the log of the inverse probability predicted by the discriminator for fake images.
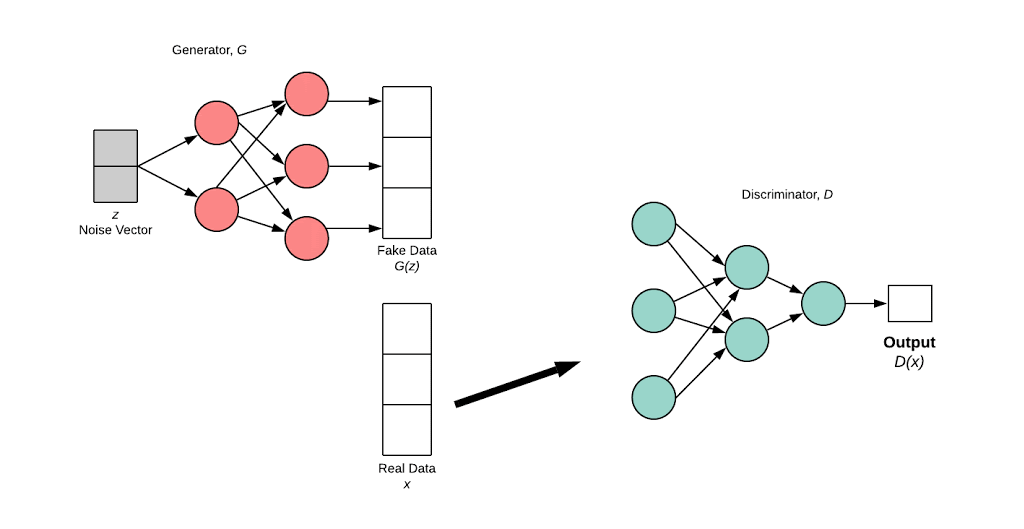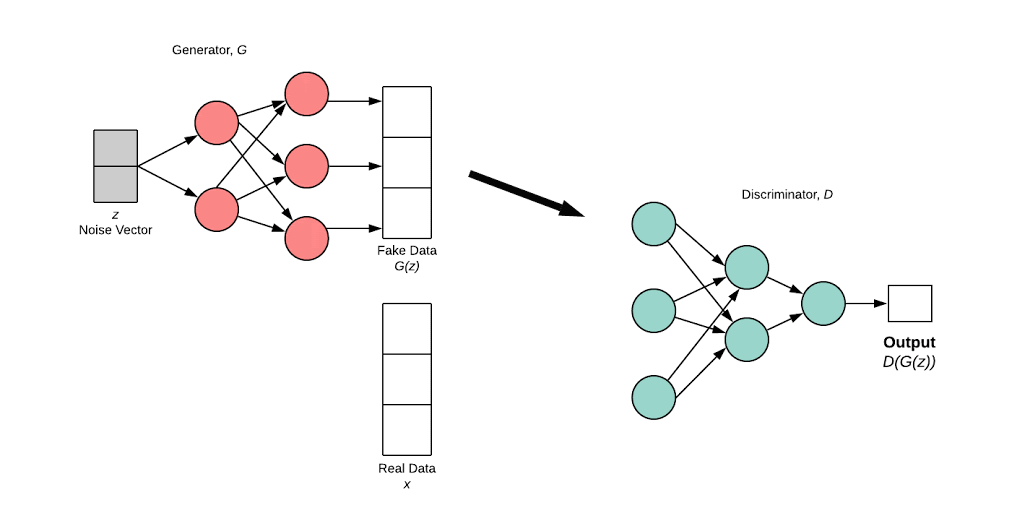
The generator’s distribution \((p_g)\) over \(x\) is defined on prior input noise variable \(p_z(z)\). A neural network framework \(G\) is defined to learn data distribution \(x\). \(G\) maps noise variable to data space as \(G(z; \theta_g)\).
\(D(x;\theta_d\) outputs a scalar. \(D(x)\) represents probability that \(x\) comes from data whereas in \(D(G(z))\) the \(G(z)\) is from generator network.
\(G\) is trained to minimize \(\log(1-D(G(z)))\). \(D\) and \(G\) plays minimax game with the value function \(V(G,D)\):
\[\min_{G}\max_{D}V(D,G) = E_{x\sim p_{data}(x)}[\log(D(x))]\;+\;E_{z\sim p_{z}(z)}[\log(D(G(z)))]\]
This adversarial training principle has transformed unsupervised task to supervised task.
Optimality
The principle of GANs is based on Nash Equilibrium. This means, theoretically, the algorithm tries to achieve global optimality \(p_g\;=\;p_{data}\)
Preposition : For \(G\) fixed, the optimal discriminator is
\[D_{G}^{\ast}(x) = \frac{p_{data}(x)}{p_{data}(x)\;+\;p_g(x)}\] Proof : To train \(D\) we maximize the value function, keeping \(G\) fixed.
\[V(G,D) = \int_{x}\;p_{data}(x)\log(D(x))dx\;+\int_{z}p_z(z)\log(1-D(g(z)))dz \] \[= \int_{x}\;p_{data}(x)\log(D(x))dx\;+\;p_g(x)\log(1-D(x)))dx \]
For any \(a,b \in R^2\) such that \(a,b \neq {0,0} \). Then the function \(f \; \rightarrow a\log(y) + b\log(1-y)\) achieves maxima at \(\frac{a}{a\;+\;b}\).
Discriminator is defined within \(supp(p_{data}) \cup supp(p_g)\)
Definition: \(supp(x)\) is the subset of the domain containing those elements that are not mapped to zero.
Training objective of discriminator can be reframed as maximum log-likelihood for estimating conditional probability \(P(Y=y\;\vert \;x)\). Thus the minmax equation can be reformulated as:
\[C(G)\; =\; \max_D V(G,D)\] \[=\;E_{x\sim p_{data}}[\log(D_G^\ast(x))]\;+\;E_{z\sim p_{z}}[\log(D_G^\ast(G(z)))]\] \[=\;E_{x\sim p_{data}}[\log(D_G^\ast(x))]\;+\;E_{x\sim p_{g}}[\log(D_G^\ast(x))]\] \[=\;E_{x\sim p_{data}}\left[\log\left(\frac{p_{data}(x)}{p_{data}(x)\;+\;p_g(x)}\right)\right]\;+\;E_{x\sim p_{g}}\left[\log\left(\frac{p_{g}(x)}{p_{data}(x)\;+\;p_g(x)}\right)\right]\]
Of Course the aim of GAN is \(p_g\;=\;p_{data}\).